Overview
Understanding and predicting the behavior of coupled natural and human systems is one of the greatest interdisciplinary research challenges of our time. As described in the introductory modeling explainer “Modeling and Socio-Environmental Systems,” socio-environmental (S-E) modeling brings many challenges—only some of which are common to other complex adaptive systems. Identifying the most important interactions and feedbacks that shape a system’s behavior is key to solving S-E problems; by reinforcing or countering these feedbacks, we can alter that system’s trajectory or outcome. Key to that is also recognizing social actions (e.g., policies, interventions targeting behaviors, etc.); causal diagramming can help with this.
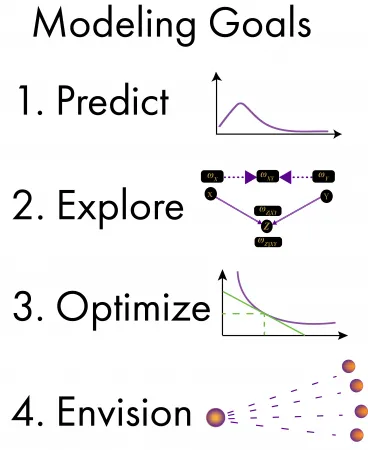
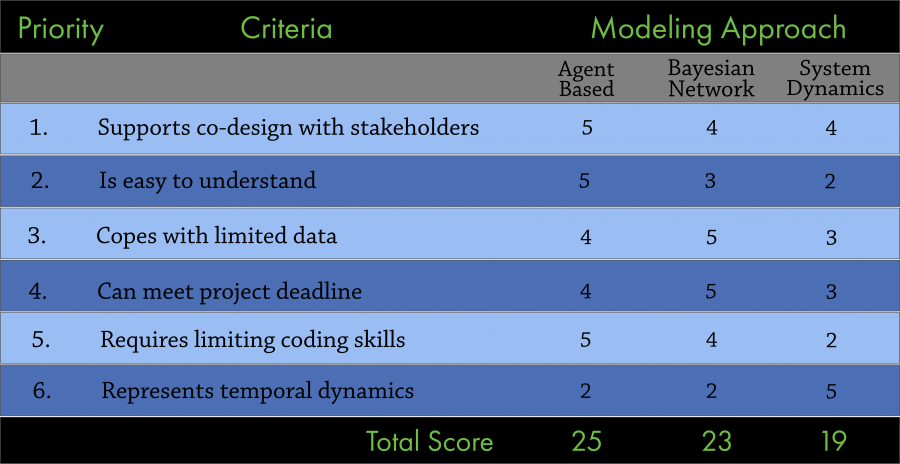
Because a wide variety of modeling approaches are available, deciding which approach to take can be daunting. Kelly et al. (2013) provides a helpful decision tree that outlines the steps in the model-selection process. In the video tutorial Selecting a Modeling Approach for Socio-Environmental Problems, Serena Hamilton describes an updated version of that process. The first step Kelly and co-authors outline is establishing the modeling requirements and constraints by answering the following questions. What are the goals of the modeling effort (e.g., system exploration, optimization of decisions, envisioning of futures)? Who are the end users—scientists with technical expertise, stakeholders, or the public? What type of output do they need? It is also important to know if there are constraints on, for example, the level of uncertainty allowed or if there are specific scales to consider.
The second step in the selection process takes the requirements and constraints of the model and turns them into multiple criteria that we can use to evaluate alternate modeling methods (Figure 2). Sometimes, organizations require the use of a specific model. Other times, models may need to be easily understandable and simple to conceptualize or parameterize for education or stakeholder-engagement purposes. Additional criteria often relate to the technical skills of the modelers and the type of data they have vs. what the modeling approach requires. The third and final step is selecting a modeling approach by evaluating and ranking specific approaches against the outlined criteria, identifying trade-offs, and deciding which criteria and associated ranks are most important to the user.
Common Modeling Approaches
Below are some commonly used types of modeling approaches, as well as some terms that are frequently encountered. For general modeling terminology, see the first explainer. Because there are entire books written about each of the approaches listed below, this list is only meant to provide a very basic overview, and so, it does not include any content on coding requirements. Some of the approaches are more suitable for the types of problems and goals S-E teams typically contend with. For each description below, we provide a few references that offer examples of those approaches’ use or other resources that expand on their use; we provide more references for the modeling approaches that are most applied to S-E problems.
Analytical Models
An analytical model has closed (exact) solutions that can be used for a general understanding of systems. These models can be solved ‘analytically’—that is, they describe a system using mathematical equations whose solutions can be found using an analytical function. The quantitative sciences often use such analytically tractable equations (and often call them “models”). Sometimes scientists use such equations to define relationships in S-E models, particularly the economic or ecological parts. Analytical approaches are very difficult to use for full S-E models because of the multiple state variables in S-E systems that interact in complex ways and lack exact solutions i.e., typically there are multiple solutions to S-E problems.
- Lafuite and Loreau (2017) modeled technological change as a logistic function in their dynamical model. They integrated measures of demography, technological change, and biodiversity to predict how time delays to species losses reduce biodiversity ecosystem services to agricultural services.
Agent-Based Models (ABMs)
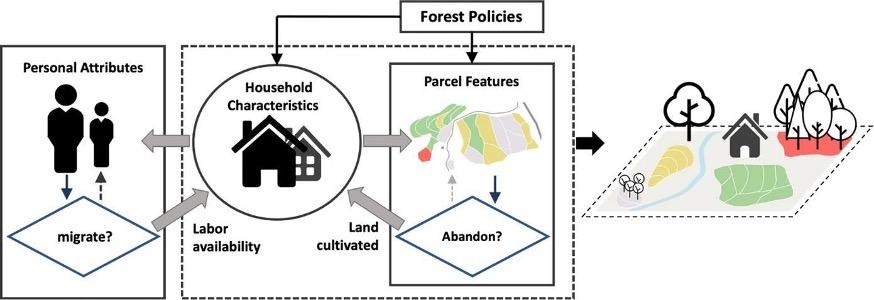
These models represent an agent or individual (sometimes called actors) whose traits or parameters occupy a range of possible values. The modeling steps rely on rules of “behavior” at the agent level. Note that agents can include groups, institutions, or any autonomous decision-making body. ABMs are useful for exploring interactions and the resulting collective behavior and for incorporating systemic change that is common in S-E systems. They highlight dynamic feedbacks, which can help in exploring potential results from different management options. They are very commonly applied to S-E systems and problems.
- Carter et al. (2020) used an ABM to study how variation in human risk perception from wildlife influences the spatial configuration of human-wildlife interactions and thus the potential design and implementation of effective conservation actions.
- Grêt-Regamey et al. (2019) used an ABM to explore the relationship between the diversity of agent behaviors (functional groups of farmers with different decision-making characteristics based on survey data) and the magnitude of ecosystem services under different price and/or climate shocks. They found that changes in land-use profit, which varied with the magnitude and type of shock imposed, influenced decisions.
- Filatova et al. (2013) reviewed the challenges, especially of agent-based modeling, particularly spatial ABMs.
- Researchers share ABMs through CoMSES Net, an open community with a common goal of improving the way we develop, share, use, and re-use agent-based and computational models for the study of social and ecological systems.
- A very introductory tutorial on agent-based modeling is available from SESYNC.
Artificial Neural Network (ANN) Models
ANN is a type of machine learning (ML) model in which data are organized by several node layers with an input layer (initial data input), an output layer, and several hidden layers of nodes that only activate at a certain threshold value. Because networks are based on ML rather than understood mechanistic relationships or specific statistical models, they are often considered black-box modeling approaches that may be useful for predicting but not understanding drivers or causation.
- Joshi and Sukumar (2021) use an ANN model to identify region-specific relationships between fire and its S-E drivers (fire-human-vegetation relationships) across the globe.
Bayesian Models
Bayesian models are a type of statistical model that focus on probability. They involve modeling not only the uncertainty of the output but also the uncertainty of the input variables and parameters. Inference comes from a “posterior probability” (also called a conditional probability) given two things: a “prior probability” and a likelihood function derived from a statistical model for newly observed data. The prior probability could be considered a hypothesis based on some knowledge or previous limited data. Say, we are interested in the probability of X given knowledge of variable a. The inference is computed based on Bayes’ theorem: P(X|a) = [P(a|X) + P(X)] / P(a). Bayesian network (BN) models also rely on use of Bayes’ theorem but include multiple random variables—some of which have conditional probabilities e.g., when X is conditional on both a and c. These are usually visually represented with a “directed acyclic graph” (a network-type diagram with links (arrows) between the variables (nodes) pointed in the direction of dependence). For the example with X, a, and b, we must compute the joint probability.
- Mayer et al. (2022) integrated environmental data on bear habitats and land use into a spatially explicit and multivariate Bayesian network model. They used this model to predict and map the tolerance to bears (probability of human-wildlife coexistence) from the view of humans (based on survey and interview data) and the risk of fitness loss from the perspective of bears (based on bear environmental habitat suitability data) in an Italian mountain range. Their Bayesian models used a set of variables that combined qualitative and quantitative components to predict the probability of human-bear co-existence.
Bio-Economic Models
These models integrate biophysical, social, and economic dynamics to understand the interplay of economic drivers like markets on environmental systems. The overlap of economic principles and theories with environmental resource dynamics gives these models added strength in understanding S-E systems. Traditionally, researchers have applied these models to optimize resource management of fisheries, but today they also use them to understand many S-E problems (e.g., those related to land use (Castro and Lechthaler 2022) and terrestrial conservation (Jean and Mouysset 2023)).
- Punt et al. 2017 combined a population dynamics model for the Tanner crab in the eastern Bering Sea with an economic model to develop sustainable fishery goals while maximizing profits. The model provided fisheries’ managers strategic advice on the likely long-term consequences of ocean acidification.
Coupled-Component Models
These models link two or more independent, usually discipline-specific models into one integrated coupled or multi-component model. These may be bioeconomic models, ABMs, system dynamics (SD), Bayesian network (BN) or other types of models that are governed individually but related. Coupled-component models are used to bring together social, economic, and biophysical models into one overall S-E model. As Kelly et al. (2013) explain: “In such cases, the biophysical models are often process-based, computationally intensive models and distributed in time and space, while the social and economic models are often the ABM, BN, SD or knowledge-based models.”
- Abebe et al. (2019) coupled an ABM of individual behavior and institutional decisions with a numerical flood model in urban environments. The ABM determines how people interact with floods (e.g., influence risk) and the flood model includes hydro-meteorological components and water infrastructure (a socio-hydrologic model).
Causal Loop Diagram (CLD)
This model is really just a visualization that shows how different variables are interrelated. Arrows between variables do not indicate a flow of materials but rather the causal influence one variable has on the other. These types of model visualizations help in illustrating feedback loops (reinforcing or balancing) in S-E systems (Banitz et al. 2022). While CLDs may be thought of as qualitative narratives or visual depictions of how a system works, researchers may translate them into a numerical form using for example a systems dynamic model. Alternatively, CLDs may be the basis for moving to a semi-quantitative model using fuzzy cognitive mapping.
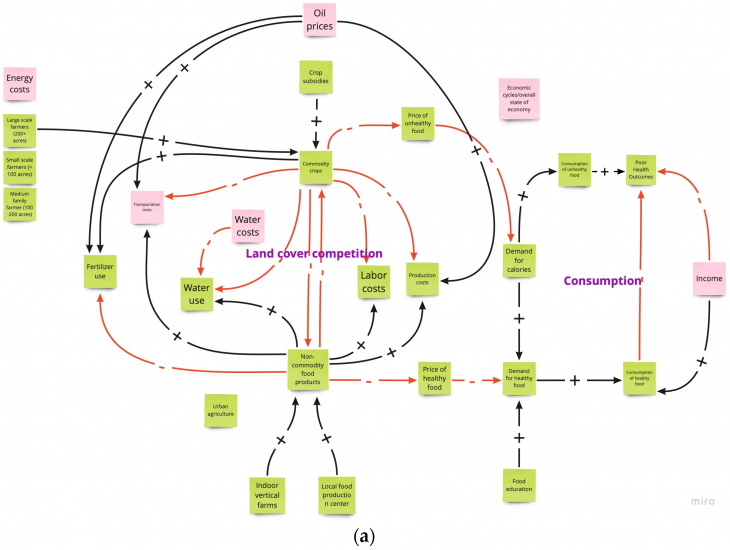
- Zellner et al. (2023) used participatory modeling workshops with stakeholders to develop CLDs of an urban-rural food, energy, and water socio-ecological system (Figure 4). Rural agricultural production, urban planning, including markets and transport systems, and energy needs planning are often not well coordinated. The team sought to enhance understanding of the connections between urban and rural components and identify potential leverage points for adaptation to climate change. Using CLD facilitated the interactions with stakeholders who are not familiar with quantitative models.
Fuzzy Cognitive Mapping (FCM) Models
This is a semi-quantitative modeling approach in which complex dynamics are simulated by assigning strengths to system relationships. This process may start with the development of a CLD and then this is parameterized using fuzzy logic in which for example, an interaction may be assigned low, medium, or high [in strength] with weights between -1 and +1 (strong negative to strong positive causality) (Castro et al. 2022).
- Alomia-Hinojosa et al. 2023 used FCM models to evaluate the perceptions of diverse groups of Nepalese farmers to changes in farm households following the addition of more livestock. Farmers simply identified positive and negative relationships of increased livestock on internal supply chains. Based on farmer survey results, the researchers identified trade-offs between increased incomes and increased labor and cost requirements for importing fodder.
Hybrid Models
These are models in which two or more modeling approaches are used. An example is using a machine learning approach to feed data into a systems model (e.g., Turgut and Bozdag 2023).
Integrated Assessment Models (IAMs)
IAMs integrate biophysical systems with economic and social decisions to help inform policy or to better understand coupled human-natural systems (e.g., climate). These models typically focus on large scales and include many submodels and coupled components that involve global change, economics, and environmental sustainability. The IPCC climate change mitigation model is an example of a process-based IAM that is used to evaluate different pathways to meeting climate change reduction goals. Such models are now being linked to high-resolution data and models of human-environmental systems at local and meso scales (Cultice et al. 2023).
Machine Learning Models
Machine learning models are based on data-mining and are created through computer algorithms. They use training data to extract patterns or relationships to make predictions on unseen datasets, where training data are from a different source or are a subset of the data that are not used in the final predictions. These models can be divided into supervised and unsupervised models. The training data use data labels or categories to train or “supervise” algorithms into classifying unseen data or predicting outcomes. The data labels may be assigned through a classification process or a regression-based approach in which both the input and output data are predetermined. Unsupervised approaches use algorithms to cluster unlabeled data sets by discovering hidden patterns in data only using the model input without considering specific output. Machine learning methods may be used for S-E problems in which there is a large amount of data available such as physical and economic data related to extractive natural resources e.g., fisheries (Letschert et al. 2023).
Network Models
Derived from graph theory, network modeling or more generally network analysis provides a mathematical approach to study relationships between different entities. Social scientists have used network models extensively to study social structure and human interactions (e.g., Tuda et al. 2021) and ecologists have used them to study food webs. Increasingly, researchers are using them for the study of full S-E systems that include both social and environmental relationships (e.g., Bodin and Tengo 2012). The nodes in the network represent the system’s components and the links between them represent relationships or interactions. Network analysis can provide insights into the dynamics of S-E systems because they can quantify changes in their structure over time or space using simple metrics. Second, they can identify critical components for control or management by, for example, identifying which component is most influential in the overall system behavior. Third, they are useful in predicting responses to perturbation, like the outcomes of shocks (e.g., for example how loss of a node or reduction in its connectivity to others affects the rest of the system).
- Sayles et al. (2019). This article provides an introduction to network analysis and why it is useful for the study of S-E systems. The authors discuss this growing research topic identifying the synergies between S-E networks and wider human-environment research then provide guidelines on the use of different S-E network approaches and models for different contexts.
- Wang et al. (2019) This article provides an example of the use of network analysis to understand the dynamics of watershed management (governance structure) and the cause of ecological degradation. Their analysis suggests a misalignment of the social and ecological structures for a transboundary river and concludes with a new governance structure that would better connect the actors of the middle and lower reaches of the river network.
Numerical Models
These models use computers to find an approximate solution to a set of equations using iterative calculations. The computers solve the set of equations over multiple time steps, resulting in the numerical solution. These models can help identify emergent system properties only emulated by running the model over many time steps and observing model output. Initial conditions or parameters in models can be varied to explore controls on systems. Numerical approaches are useful for many types of models (e.g., system dynamics, analytical models).
- Knighton et al. (2021) extended an existing socio-hydrologic model to ask how hydrological flood hazards interact with human exposure and vulnerability and resilience (how well people recover, learn from, and adapt to past floods) to characterize flood-human interactions in U.S. cities. The model was calibrated with local data and the model’s equation set solved numerically.
- Pal and Ghosh (2023) developed a S-E model describing forest cover, human population size, and the socioeconomics of human behavior (opinion on forest conservation that affects tree harvests) as a dynamic variable. They were interested in how these relate to CO2 levels and applied both analytical and numerical solutions for comparison.
Process-Based Models
Also known as mechanistic models, these models are based on some understanding of how a system works and can be used to identify causation. These models use equations that represent the processes that govern change (i.e., they are theoretically based)—as opposed to using a statistical description of change based on data. Examples were provided above (e.g., see equations in papers listed under numerical and analytical). Many of the equations can be solved analytically.
Statistical Models
A mathematical “model” that relies on the statistical probability of some random variable assumed to be sampled normally and that represents the population of all random variables. Model is in quotes since this approach usually refers to a statistical analysis, and the “modeling” aspect is the structure of the statistical equation (i.e., which variables are used and how they are related). For example, Ordónez Barona et al. (2023) use a regression-based approach with a structural equation model technique to show that more contact among people in some Latin American and Caribbean cities resulted in more participation in collective decision making and more optimistic views about the state of urban forest management and governance.
Scenario (Futures) Models
Rather than projections, scenario modeling uses plausible ‘packages’ of simultaneous social and environmental conditions or inputs. Exact conditions in scenario modeling are often unknown; therefore, they require a range of possible values or an ensemble of ‘packages’ that reasonably represent the system at the desired time or condition. These models are used to facilitate communication and identify desirable or likely futures (S-E conditions or states), as well as potential system responses to new policies or management designs. Even more so than some forms of S-E modeling, scenario models require a highly participatory approach to development in which diverse stakeholders work iteratively with modelers. Typically, they involve use of both qualitative and quantitative data/information (e.g., Booth et al. 2016). This tutorial by modelers Vanessa Schweizer and Hannah Kosow explains well developed methods for the development process.
- Roura‑Pascual et al. (2021) used a participatory approach to gather expert knowledge to create plausible scenarios of biological invasions globally. The goal was to use the scenarios to identify future drivers for use in IAMs simulating the effects of land use, energy consumption, and resulting greenhouse gases under different policies. Economics and global trade especially in the context of climate change were part of the scenario process.
- Hallberg-Sramek et al. 2023 engaged stakeholders to combine scenario modeling and a quantitative scenario analysis based on the stakeholders’ preferences regarding ecosystem services from Swedish forests. Based on the preferences, they explored four forest-management scenarios (close to nature, class management, maximizing harvest, and combined) then used a simulation model for scenario analyses and then received feedback from the stakeholders on the results of those analyses.
Systems Dynamical Models
These are models with multiple, interacting components, and they are typically based on systems of differential or difference equations and logic functions to dictate what and when certain equations are used. Extensively used for ecosystem modeling, where they represent a system of “stocks” (components) and “flows” (relationships between components), these are also commonly applied to S-E problems. They are useful in helping to integrate diverse types of data and understand how feedbacks produce nonlinearities in complex systems (Allington et al. 2018).
- Elsawah et al. (2017) is a very useful resource. It provides an overview of modeling socio-ecological systems using a system dynamics approach. It covers the issues modelers face during the modeling process and provides guidance on effective design and implementation of system dynamics models. These models are illustrated very concretely, drawing from the lessons learned from five case studies.
- Allington et al. (2018) studied pastoral systems on the Mongolian plateau to understand how climatic and socioeconomic forces interact to influence human-decision making regarding land use and resource management of rangelands. Models were fit with differential equations and parameters estimated based on primary sources, the literature, and functions derived during researcher workshops. They compared the projections for different system variables (e.g., grassland area, livestock size) under different alternative scenarios.
- Roobavannan et al. (2020) used a systems dynamic-based approach for socio-hydrologic modeling of economic diversification in an Australian agricultural and industrial watershed that can increase sustainability under future climates. Changes in social decisions on water allocation and release of river flows to support ecosystems resulted from varying community sensitivity to the economic repercussions from agricultural vs industrial growth.